2. Introduction to Gromacs¶

Learning goals:
To learn the basic structure and protocols of Gromacs
To understand that different software employ different unit systems
Keywords: Gromacs, grompp, molecular dynamics, molecular topology, force field, interactions, free energy, thermostat, barostat, QM/MM, unit system, CUDA
Associated material:
2.1. What is Gromacs¶
Gromacs [6][25][41][5][39][2] is simulation software package for classical MD simulations. Along with NAMD [32][36], Amber [12] and LAMMPS [37], it is one of the world’s most popular MD simulation packages. Although it was originally developed for simulations of biochemical systems such as proteins, lipids and nucleic acids, it is a general purpose simulation package and has been used for nanotubes, colloids, polymers and many other systems. It has been used to simulate systems with millions of particles. Gromacs has a very rich feature set that goes far beyond what we can discuss during this course, see, for example [10][38].
The name Gromacs is originally an acronym, that stands for the Groningen Machine for Chemical Simulations. The development started in 1991. It was originally developed in the group of Herman Berendsen at the University of Groningen in the Netherlands. Since around 2001, the main Gromacs development has been done at the Royal Institute of Technology (Kungliga Tekniska högskolan, KTH) in Stockholm, Stockholm University and Uppsala University, all in Sweden. Gromacs is also part of the European Union BioExcel (Centre of Excellence for Computational Biomolecular Research) program and it is open source. Notably, essentially all of the major simulation packages are open source.
2.1.1. Relation of Gromacs to other MD simulation packages¶
There are many excellent software packages available for classical MD simulations. Some of the most famous ones in addition to Gromacs are Amber (Assisted Model Building with Energy Refinement), NAMD (Nanoscale Molecular Dynamics), CHARMM (Chemistry at Harvard Macromolecular Mechanics) [8], LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator), GROMOS (GROningen MOlecular Simulation; one of the oldest packages as it dates back to 1978) and DL-Poly (not sure about the acronym, but it is likely that DL refers to Daresbury Laboratory where DL-Poly originated from the group of William Smith around 1993). They all have their own particular strengths and the choice depends on the task at hand, simulation conditions, force field requirements, resources and prior experience. Gromacs, NAMD, Amber and LAMMPS offer GPU acceleration which allows for simulations of moderate size systems (10,000’s of atoms) even on consumer PCs with (currently NVIDIA) graphics cards.
The need for a particular force field is another important criterion when choosing software. Some of the above software packages are restricted to only a certain family for force fields (CHARMM and NAMD software for CHARMM family of force fields and Amber software for Amber family of force fields). One particular strength of Gromacs is that it supports a very wide range of force fields including atomistic (Amber [46], CHARMM [26][45][19], OPLS [7], GROMOS [40] force field families) and coarse-grained (MARTINI) [10]. There are also user-provided patches to some versions of Gromacs that support more exotic force fields such as PLUM[4]. On the other hand, a package such as Amber may offer support to the very latest Amber-family force fields that are not yet available for other software.
2.1.2. Common point of confusion: Force field vs software¶
When reading literature, one issue that often causes confusion is the naming of force fields and software. The names Amber, CHARMM and GROMOS can refer to either software or force field (or both). When taking about either, ones should use the software and force field version numbers as that makes the situation much clearer. This is also important from another point of view: Each of the force fields has many variants and it is very important to distinguish between them. To give an idea, CHARMM force fields include (and this is not a complete list) CHARMM22, CHARMM27, CHARMM36 [23], CHARMM36m [19], CHARMM36 Drude [24], CGenFF, CHARMM27/CMAP and so on.
More: List of software for molecular mechanics
Comparison of software for molecular mechanics modeling from Wikipedia
A list of Molecular dynamics software from Wikipedia
It is important to keep in mind that there is no best choice when it comes to software. The choice depends on many factors such as one needs for some specific functionality, needs for specific force fields, available hardware and so on as discussed before. The good news is that there are a lot of excellent choices such as those mentioned above (and there is more). Here, we use Gromacs.
2.2. Main features of Gromacs¶
Gromacs has always been known for it is very good performance, stability and its developers have always been quick to adapt new technologies such as SSE (Streaming SIMD extensions) and SSE2 in the early 2000’s and later CUDA-based GPU acceleration. From the user point of view, Gromacs is run from the command line (CLI) - this is the case with essentially all of the simulations software. Gromacs has been ported to various computer architectures and, importantly, both input and output files are independent of the hardware that was used to generate them. Input files are given in ASCII format (this is also the reason why we need an ASCII editor such as vi, emacs, atom or such to edit the input files).
Gromacs saves data in compressed form with two options (.xtc and .trr; we will discuss the Gromacs files in a separate section below). Gromacs also provides a very large set (>100) of built-in analysis routines. The use of these routines typically require two steps:
identification of the atoms and/or molecules of interest. This is called indexing and it produces and index file (
.ndx). This index file is then used inrunning the actual analysis routine.
Both of these steps must be done on command line or, alternatively, using Python. There are several Python packages available, but the personal biased reference here is the very versatile MDAnalysis package [31].
There are also several independent (mostly Python-based) packages that can read and analyze Gromacs output data. Examples of such packages include VMD [4], PyMOL, MDAnalysis [31], FATSLiM [9] and PyBILT. Importantly, MDAnalysis can also be used to analyze trajectories produced by many other simulation software including NAMD and Amber.
Gromacs, like most of the main simulation software, can be run on serial, parallel and GPU systems. For parallelization, it supports MPI and OpenMP and parallelization across multiple GPUs. Both NVIDIA’s CUDA and OpenCL are supported but former offers much better performance. There are a few consequences:
If you have a multicore laptop or desktop, you can run parallel simulations even on your own computer.
If you have an NVIDIA GPU, you can use it to run Gromacs simulations provided you are running Linux. The ability of being able to use GPUs from WSL2 is being added but it is not yet (Dec. 2020) generally available. This is also important for tasks other than molecular simulations as GPU acceleration is available for, for example, the Tensorflow package for machine learning.
2.3. Quantum Mechanical / Molecular Mechanics calculations (QM/MM)¶
Gromacs also allows for hybrid QM/MM simulations: In QM/MM, most of the simulation is done at the classical level, but a small part of the system (that is, a subsystem) is handled quantum mechanically. This requires coupling Gromacs with a quantum mechanical simulation package. At this time Gromacs has interfaces at least with CPMD, Gaussian and GAMESS-UK. Support is also planned for CP2K in 2021.
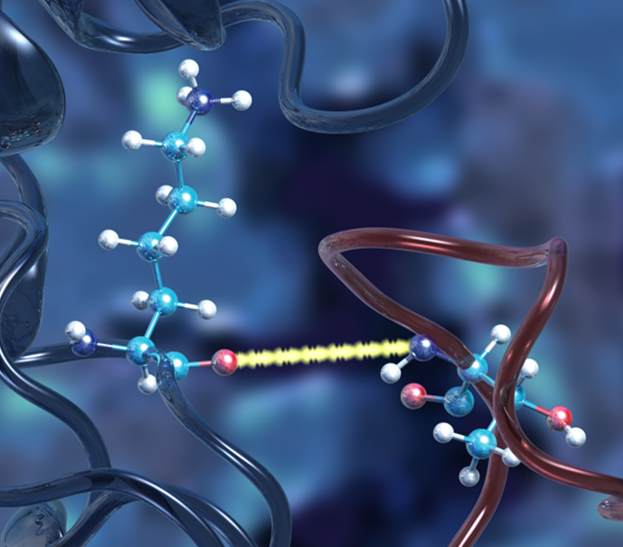
Fig. 2.13 In a QM/MM simulation, most of the system is described using classical Newtonian dynamics but a small area, indicated here by the yellow line connecting two atoms, is described quantum mechanically. There are some challanges: how to transfer the information between the parts that are treated quantum mechanically and classically, and how to match the time scales. As for the former, the fundamental questions relate to Ehrenfest theorem and for the latter the fundamental issue is that quantum events occur in time scales that are much faster than in classical mechanics and involve electrons that are not present at the classical level. Although the idea of QM/MM simulations dates back to the end of the 1960’s and a lot of progress has been made including the Nobel Prize in Chemistry in 2013, many fundamental questions remain unresolved.¶
2.4. The grompp preprocessor¶
One particular feature of Gromacs’ is the grompp preprocessor. grompp is used at several stages of building a simulation, but in general it reads the file describing molecular topologies (.top), it checks the validity and consistency of files and builds a binary run input file (.tpr) that is used for execution of the MD simulation.
Technically, grompp is serial preprocessor and it is used to perform several tasks prior to the actual simulation. In particular, grommp is used for the following tasks:
To read the molecular topology file (
.top). Then,gromppchecks its validity, and (if everything is ok), it expands the topology from a molecular to an atomic description. That is, it builds the molecules using the atomic data.To read the coordinate file. Additionally, it can generate velocities from a Maxwellian distribution if requested in the input (
.mdp) file.To reads parameters (from the
.mdpfile). This includes the number of MD time steps, time step, cut-off and so on.To use some of Gromacs’ utility programs. This includes generating the simulation box, adding ions, processing Protein Databank (
.pdb) files
2.5. Additional features¶
It is impossible to give a brief yet comprehensive description of the many features that Gromacs offers. Below, some of the common ones are listed as examples. The listed features are chosen based on what will be encountered in the simulations during this course, but there are many more.
For integration of Newton’s equations of motion, there are a few options most notably the velocity-Verlet and the leap-frog methods.
For energy minimization, the main options are the method of steepest descents and the conjugate gradient method.
There is an often overlooked major difference between integration of the equations of motion and energy minimization: Integration is the propagation of the equations of motion in time with a time step given in terms of real time. Thus, it involves updates of the particles’ positions and velocities. Energy minimization using steepest descents or the conjugate gradient method is a mathematical (deterministic) optimization process that involves minimization of the potential energy, that is, only positions are needed. Second, even though ones gives a number of steps for the optimization process, the number of steps does not correspond to physical time but only gives an upper limit for the number of steps to be taken in case the process doesn’t converge earlier. We will not discuss these methods in detail here, but it is important to understand that optimization using these methods does not involve time or velocities, it is simply minimization of the potential energy. This is a general feature of these methods are not specific to Gromacs or any other simulation/modeling package.
For thermostats, Gromacs offers the Berendsen [5], Nosé-Hoover [34][33][18], Nosé-Hoover chain[28] (with some restrictions), v-rescale[11], Andersen [2] and Langevin [16] (called stochastic dynamics in Gromacs) thermostats. Currently, the Dissipative Particle Dynamics (DPD) thermostat is not available (it is available in LAMMPS). The choice of thermostat depends on the system and properties of interest, but the Nosé-Hoover and v-rescale are the most common and recommended choices. For colloidal systems, Gromacs has also Brownian dynamics.
For periodic boundary conditions, Gromacs has three options for geometry, cuboid, rhombic dodecahedron and truncated octahedron.
Why those ones for periodic boundary conditions? The reason is simple: When using periodic boundaries, the simulation cell must have a structure that it is space filling. If the simulation uses closed boundaries, any structure is fine (as long as it is available in the code or if one can code it).
For barostats, Gromacs has the Berendsen[5], Parrinello-Rahman[35] and Martyna-Tuckerman-Tobias-Klein[29][30] (with some restrictions) as the possible options. The two latter ones are the recommended options, but the Berendsen method is often useful during the pre-equilibration of the system.
For computing the long-range electrostatic interactions, one has the choices of simple cutoff (not recommended), reaction-field [42], plain Ewald summation [14], the particle-particle particle-mesh (P3M) and the particle mesh Ewald sum (PME) [13]. The last one is the most common choice. Gromacs has also the option to use a modified PME for systems that are not fully periodic. The most additions (not in the main version at this time) is the Fast Multipole Method (FMM) of Greengard and Rokhlin [15].
Fig. 2.14 Examples of space filling and non-space filling strcutures in two dimensions. Round (and spherical in 3d) objects can be used to make non-space filling fractals called Apollonian nets. Such structures are important in studies of granular materials. Bravais lattices are space filling. In 2d there are 5 Bravais lattices, square (tetragonal), rectangular (orthorhombic) and hexagonal being the relevent ones in this context. In 3d there are 14 Bravais lattices.¶
2.5.1. Free energy calculations¶
Gromacs also supports free energy calculations using the slow growth method, thermodynamic integration and umbrella sampling. Metadynamics [22][44] with its many variants can be used using the PLUMED-plugin. PLUMED [7][3][43] is not restricted to Gromacs but it can be used with many other packages including LAMMPS, Amber, CP2K (quantum) and so on. PLUMED was originally introduced in 2009 [7] and its current version is PLUMED2[43].
But what is free energy? These may sound familar:
Gibbs free energy: \(G = H- TS\)
Enthalpy: \(H = U + pV\)
Helmholz free energy: \(F = U -TS \)
In the above, \(T\) is temperature, \(S\) is entropy, \(p\) is pressure, \(V\) is volume, and \(U\) is internal energy. We will discuss free energy in detail in some of the next lectures.
2.6. Gromacs unit system¶
Every MD software has its own convention to handle units. When switching between, for example, Gromacs, NAMD, LAMMPS or others, one should pay attention to the units used in each of the software. Another circumstance in which the importance of the unit convention should be give special attention is when different analysis packages such as VMD and MDAnalysis or such are used. They may (and often do) use different convention(s).
Gromacs uses the following five base units:
Quantity: |
Unit: |
Numerical value: |
|---|---|---|
length: |
nanometers |
10\(^{-9}\) m |
time: |
picoseconds |
10\(^{-12}\) s |
temperature: |
kelvin |
absolute scale: 0 K = -273.15 \(^\circ\)C |
mass: |
u (atomic unit) |
\(\approx\) 1.661 \(\times\) 10\(^{-27}\) kg |
charge |
elementary charge (e) |
\(\approx\) 1.602 \(\times\) 10\(^{-19}\) C |
This gives the following derived units:
Quantity: |
Unit: |
|---|---|
energy: |
kJ/mol |
force: |
kJ/(mol \(\times\) nm ) |
velocity: |
nm/ps |
density: |
g/mol |
pressure: |
bar |
dipole moment: |
e \(\times\) nm |
electric field: |
kJ/( mol \(\times\) nm \(\times\) e) |
electric potential: |
kJ/( mol \(\times\) e) |
compressibility: |
bar\(^{-1}\) |
2.7. References¶
- 2
Mark James Abraham, Teemu Murtola, Roland Schulz, Szilárd Páll, Jeremy C. Smith, Berk Hess, and Erik Lindahl. GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX, 1-2:19–25, sep 2015. doi:10.1016/j.softx.2015.06.001.
- 2
Hans C. Andersen. Molecular dynamics simulations at constant pressure and/or temperature. The Journal of Chemical Physics, 72(4):2384–2393, feb 1980. doi:10.1063/1.439486.
- 3
Alessandro Barducci, Massimiliano Bonomi, and Michele Parrinello. Metadynamics. Wiley Interdisciplinary Reviews: Computational Molecular Science, 1(5):826–843, Sep 2011. doi:10.1002/wcms.31.
- 4
Tristan Bereau, Zun-Jing Wang, and Markus Deserno. More than the sum of its parts: coarse-grained peptide-lipid interactions from a simple cross-parametrization. The Journal of Chemical Physics, 140(11):115101, Mar 2014. doi:10.1063/1.4867465.
- 5(1,2)
H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. Molecular dynamics with coupling to an external bath. The Journal of Chemical Physics, 81(8):3684, 1984. doi:10.1063/1.448118.
- 6
H.J.C. Berendsen, D. van der Spoel, and R. van Drunen. Gromacs: a message-passing parallel molecular dynamics implementation. Computer Physics Communications, 91(1-3):43–56, Sep 1995. doi:10.1016/0010-4655(95)00042-e.
- 7(1,2)
Massimiliano Bonomi, Davide Branduardi, Giovanni Bussi, Carlo Camilloni, Davide Provasi, Paolo Raiteri, Davide Donadio, Fabrizio Marinelli, Fabio Pietrucci, Ricardo A. Broglia, and Michele Parrinello. PLUMED: A portable plugin for free-energy calculations with molecular dynamics. Computer Physics Communications, 180(10):1961–1972, oct 2009. doi:10.1016/j.cpc.2009.05.011.
- 8
Bernard R. Brooks, Robert E. Bruccoleri, Barry D. Olafson, David J. States, S. Swaminathan, and Martin Karplus. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. Journal of Computational Chemistry, 4(2):187–217, 1983. doi:10.1002/jcc.540040211.
- 9
Sébastien Buchoux. FATSLiM: a fast and robust software to analyze MD simulations of membranes. Bioinformatics, 33(1):133–134, aug 2016. doi:10.1093/bioinformatics/btw563.
- 10
Giovanni Bussi. Hamiltonian replica exchange in gromacs: a flexible implementation. Molecular Physics, 112(3-4):379–384, aug 2013. doi:10.1080/00268976.2013.824126.
- 11
Giovanni Bussi, Davide Donadio, and Michele Parrinello. Canonical sampling through velocity rescaling. The Journal of Chemical Physics, 126(1):014101, 2007. doi:10.1063/1.2408420.
- 12
David A. Case, Thomas E. Cheatham, Tom Darden, Holger Gohlke, Ray Luo, Kenneth M. Merz, Alexey Onufriev, Carlos Simmerling, Bing Wang, and Robert J. Woods. The amber biomolecular simulation programs. Journal of Computational Chemistry, 26(16):1668–1688, 2005. doi:10.1002/jcc.20290.
- 13
Tom Darden, Darrin York, and Lee Pedersen. Particle mesh ewald: an n·log(n) method for ewald sums in large systems. The Journal of Chemical Physics, 98(12):10089–10092, jun 1993. doi:10.1063/1.464397.
- 14
P. P. Ewald. Die berechnung optischer und elektrostatischer gitterpotentiale. Annalen der Physik, 369(3):253–287, 1921. doi:10.1002/andp.19213690304.
- 15
L. Greengard and V. Rokhlin. A fast algorithm for particle simulation. Journal of Computational Physics, 135(2):280–292, aug 1997. doi:10.1006/jcph.1997.5706.
- 16
Gary S. Grest and Kurt Kremer. Molecular dynamics simulation for polymers in the presence of a heat bath. Physical Review A, 33(5):3628–3631, may 1986. doi:10.1103/physreva.33.3628.
- 5
Berk Hess, Carsten Kutzner, David van der Spoel, and Erik Lindahl. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. Journal of Chemical Theory and Computation, 4(3):435–447, Mar 2008. doi:10.1021/ct700301q.
- 18
William G. Hoover. Canonical dynamics: equilibrium phase-space distributions. Physical Review A, 31(3):1695–1697, mar 1985. doi:10.1103/physreva.31.1695.
- 19(1,2)
Jing Huang, Sarah Rauscher, Grzegorz Nawrocki, Ting Ran, Michael Feig, Bert L de Groot, Helmut Grubmüller, and Alexander D MacKerell. CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nature Methods, 14(1):71–73, nov 2016. doi:10.1038/nmeth.4067.
- 4
William Humphrey, Andrew Dalke, and Klaus Schulten. VMD: visual molecular dynamics. Journal of Molecular Graphics, 14(1):33–38, Feb 1996. doi:10.1016/0263-7855(96)00018-5.
- 7
William L. Jorgensen and Julian Tirado-Rives. The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin. Journal of the American Chemical Society, 110(6):1657–1666, mar 1988. doi:10.1021/ja00214a001.
- 22
A. Laio and M. Parrinello. Escaping free-energy minima. Proceedings of the National Academy of Sciences, 99(20):12562–12566, October 2002. doi:10.1073/pnas.202427399.
- 23
Sarah Lee, Alan Tran, Matthew Allsopp, Joseph B. Lim, Jérôme Hénin, and Jeffery B. Klauda. CHARMM36 united atom chain model for lipids and surfactants. The Journal of Physical Chemistry B, 118(2):547–556, jan 2014. doi:10.1021/jp410344g.
- 24
Fang-Yu Lin, Jing Huang, Poonam Pandey, Chetan Rupakheti, Jing Li, Benoı\^t Roux, and Alexander D. MacKerell. Further optimization and validation of the classical drude polarizable protein force field. Journal of Chemical Theory and Computation, 16(5):3221–3239, apr 2020. doi:10.1021/acs.jctc.0c00057.
- 25
Erik Lindahl, Berk Hess, and David van der Spoel. GROMACS 3.0: a package for molecular simulation and trajectory analysis. Journal of Molecular Modeling, 7(8):306–317, aug 2001. doi:10.1007/s008940100045.
- 26
Alexander D. MacKerell, Nilesh Banavali, and Nicolas Foloppe. Development and current status of the CHARMM force field for nucleic acids. Biopolymers, 56(4):257–265, 2000. doi:10.1002/1097-0282(2000)56:4<257::aid-bip10029>3.0.co;2-w.
- 10
Siewert J. Marrink, H. Jelger Risselada, Serge Yefimov, D. Peter Tieleman, and Alex H. de Vries. The MARTINI force field: coarse grained model for biomolecular simulations. The Journal of Physical Chemistry B, 111(27):7812–7824, jul 2007. doi:10.1021/jp071097f.
- 28
Glenn J. Martyna, Michael L. Klein, and Mark Tuckerman. Nose’–hoover chains: the canonical ensemble via continuous dynamics. The Journal of Chemical Physics, 97(4):2635, 1992. doi:10.1063/1.463940.
- 29
Glenn J. Martyna, Douglas J. Tobias, and Michael L. Klein. Constant pressure molecular dynamics algorithms. The Journal of Chemical Physics, 101(5):4177–4189, sep 1994. doi:10.1063/1.467468.
- 30
Glenn J. Martyna, Mark E. Tuckerman, Douglas J. Tobias, and Michael L. Klein. Explicit reversible integrators for extended systems dynamics. Molecular Physics, 87(5):1117–1157, apr 1996. doi:10.1080/00268979600100761.
- 31(1,2)
Naveen Michaud-Agrawal, Elizabeth J. Denning, Thomas B. Woolf, and Oliver Beckstein. MDAnalysis: a toolkit for the analysis of molecular dynamics simulations. Journal of Computational Chemistry, 32(10):2319–2327, apr 2011. doi:10.1002/jcc.21787.
- 32
Mark T. Nelson, William Humphrey, Attila Gursoy, Andrew Dalke, Laxmikant V. Kalé, Robert D. Skeel, and Klaus Schulten. NAMD: a parallel, object-oriented molecular dynamics program. The International Journal of Supercomputer Applications and High Performance Computing, 10(4):251–268, dec 1996. doi:10.1177/109434209601000401.
- 33
Shuichi Nosé. A unified formulation of the constant temperature molecular dynamics methods. The Journal of Chemical Physics, 81(1):511–519, jul 1984. doi:10.1063/1.447334.
- 34
Shūichi Nosé. A molecular dynamics method for simulations in the canonical ensemble. Molecular Physics, 52(2):255–268, Jun 1984. doi:10.1080/00268978400101201.
- 35
M. Parrinello and A. Rahman. Polymorphic transitions in single crystals: a new molecular dynamics method. Journal of Applied Physics, 52(12):7182–7190, dec 1981. doi:10.1063/1.328693.
- 36
James C. Phillips, David J. Hardy, Julio D. C. Maia, John E. Stone, João V. Ribeiro, Rafael C. Bernardi, Ronak Buch, Giacomo Fiorin, Jérôme Hénin, Wei Jiang, Ryan McGreevy, Marcelo C. R. Melo, Brian K. Radak, Robert D. Skeel, Abhishek Singharoy, Yi Wang, Beno\^ıt Roux, Aleksei Aksimentiev, Zaida Luthey-Schulten, Laxmikant V. Kalé, Klaus Schulten, Christophe Chipot, and Emad Tajkhorshid. Scalable molecular dynamics on CPU and GPU architectures with NAMD. The Journal of Chemical Physics, 153(4):044130, jul 2020. doi:10.1063/5.0014475.
- 37
Steve Plimpton. Fast parallel algorithms for short-range molecular dynamics. Journal of Computational Physics, 117(1):1–19, Mar 1995. doi:10.1006/jcph.1995.1039.
- 38
René Pool, Jaap Heringa, Martin Hoefling, Roland Schulz, Jeremy C. Smith, and K. Anton Feenstra. Enabling grand-canonical monte carlo: extending the flexibility of GROMACS through the GromPy python interface module. Journal of Computational Chemistry, pages n/a–n/a, 2012. doi:10.1002/jcc.22947.
- 39
S. Pronk, S. Pall, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, and et al. Gromacs 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics, 29(7):845–854, Feb 2013. doi:10.1093/bioinformatics/btt055.
- 40
Maria M. Reif, Moritz Winger, and Chris Oostenbrink. Testing of the GROMOS force-field parameter set 54a8: structural properties of electrolyte solutions, lipid bilayers, and proteins. Journal of Chemical Theory and Computation, 9(2):1247–1264, jan 2013. doi:10.1021/ct300874c.
- 41
David Van Der Spoel, Erik Lindahl, Berk Hess, Gerrit Groenhof, Alan E. Mark, and Herman J. C. Berendsen. GROMACS: fast, flexible, and free. Journal of Computational Chemistry, 26(16):1701–1718, 2005. doi:10.1002/jcc.20291.
- 42
Ilario G. Tironi, René Sperb, Paul E. Smith, and Wilfred F. van Gunsteren. A generalized reaction field method for molecular dynamics simulations. The Journal of Chemical Physics, 102(13):5451–5459, apr 1995. doi:10.1063/1.469273.
- 43(1,2)
Gareth A. Tribello, Massimiliano Bonomi, Davide Branduardi, Carlo Camilloni, and Giovanni Bussi. PLUMED 2: new feathers for an old bird. Computer Physics Communications, 185(2):604–613, feb 2014. doi:10.1016/j.cpc.2013.09.018.
- 44
Omar Valsson, Pratyush Tiwary, and Michele Parrinello. Enhancing important fluctuations: rare events and metadynamics from a conceptual viewpoint. Annual Review of Physical Chemistry, 67(1):159–184, may 2016. doi:10.1146/annurev-physchem-040215-112229.
- 45
K. Vanommeslaeghe and A.D. MacKerell. CHARMM additive and polarizable force fields for biophysics and computer-aided drug design. Biochimica et Biophysica Acta (BBA) - General Subjects, 1850(5):861–871, may 2015. doi:10.1016/j.bbagen.2014.08.004.
- 46
Junmei Wang, Romain M. Wolf, James W. Caldwell, Peter A. Kollman, and David A. Case. Development and testing of a general amber force field. Journal of Computational Chemistry, 25(9):1157–1174, 2004. doi:10.1002/jcc.20035.