1. What is Molecular Dynamics (MD)¶
Learning goals:
To learn the basic MD workflow
To understand the concept of boundary conditions
To understand the process of initialization in MD simulations
To understand the concepts of energy minimization, pre-equilibration, equilibration and production run
To be able to estimate the number of molecules or/and atoms that can be put in a simulation box.
Keywords: Molecular dynamics, workflow, molecular topology, force field, boundary conditions, initialization, equilibration, simulation box
Now it is time to discuss some of the basic concepts of MD. As this is the first description, it does not aim to be complete, but rather practical in the sense that basic concepts and terminology is introduced. The aim is that this knowledge helps us to start analyzing some data and setting up simulations. These concepts (as we well as several new ones) will be elaborated as we progress.
1.1. Workflow in MD simulations¶
The basic workflow can be described as follows:
Fig. 1.11 General MD workflow independent of software. First, one must define the components, that is, the atoms and molecules and their interactions. The atoms and molecules are then used to create the simulation system. After the simulation system has undergone relaxation and pre-equilibration, the actual MD simulation can be started. The simulation produces a trajectory - the coordinates (velocities and forces can be also saved) of all of the particles as a function of time. This trajectory is used for data analysis.¶
1.2. MD workflow refined¶
The previous figure showed the basic parts. However, each of the parts consists of small parts that are vital in setting up MD simulations. The figure below shows some of the most important parts. Importantly, these are not specific to any particular software. The same workflow and issues are present independent of software. Which part involves the most work depends on various matter such as if new molecules need to be parameterized, is the system multicomponent, are special techniques required and so on.
Fig. 1.12 General MD workflow independent of software. The different colors and blocks indicate the structure: First, one must define the components, that is, the atoms and molecules and their interactions. If we only individual atoms, then the topology, or connectedness is simple: there is none and the interactions between the atoms are non-bonded. In molecules, the atoms composing a molecule are connected and we must describe the their connectedness. This is involves numbering the atoms in a systematic way and providing information about how they are connected. This gives rise to bonded interactions. The force field, that is, the description of all interactions and parameters, and topology define the molecules. When a system is composed, one also needs to provide the initial coordinates.¶
1.3. Initialization¶
The system needs to be set up before the actual simulation can start. Assuming that a force field has been chosen, one needs to set up the simulation system. 1) This means assembling the system in a simulation box and 2) choosing the boundary conditions. The first part involves assigning initial coordinates for the atom and molecules. There are several possibilities for doing that. What is the most appropriate method depends on the system. For example: To create a system resembling a liquid or a gas, random generation of coordinates may be a good choice whereas for a solid-state system one may want to choose a lattice. For protein simulations, the most convenient choice may be to download a PDB file from the PDB database (PDB files have molecular coordinates). Such data may come, for example, from X-ray diffraction or NMR. Similarly, one may generate the homology models based on experimental data and use the initial coordinates from one/some of the homology model(s). Finally, a very common choice is to use coordinates data from a previous simulation.
1.4. Energy minimization vs equilibration vs production simulation¶
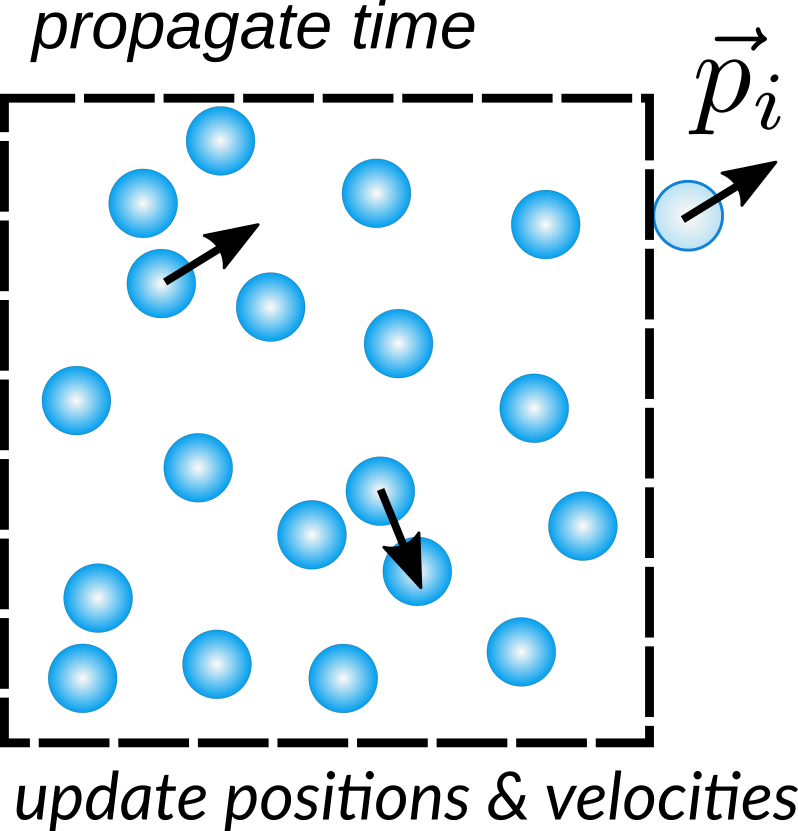
There is an often overlooked major difference between integration of the equations of motion and energy minimization: Integration is the propagation of the equations of motion in time with a time step given in terms of real time. Thus, it involves updates of the particles’ positions and velocities. Energy minimization using steepest descents or the conjugate gradient method is a mathematical (deterministic) optimization process that involves minimization of the potential energy, that is, only positions are needed. Second, even though ones gives a number of steps for the optimization process, the number of steps does not correspond to physical time but only gives an upper limit for the number of steps to be taken in case the process doesn’t converge earlier. We will not discuss these methods in detail here, but it is important to understand that optimization using these methods does not involve time or velocities, it is simply minimization of the potential energy. This is a general feature of these methods are not specific to Gromacs or any other simulation/modeling package.
Further considerations:
If one has to assemble a system consisting of several different molecules, it is usually a good idea to start from the largest molecule first. For example, take the protein and put in the simulation box. After that, solvate the system with water molecules and add the ions (if needed) last.
If one continues one’s own previous simulation of the same system, then one can jump directly to the production phase and the time is continued from the end of the previous simulations. Most software provide mechanisms for that
It is generally a good idea to use a previous simulation as a starting point since it has been already run for possibly a long time. It may still be a good idea to go through the equilibration phase and double-check that the system is indeed in equilibrium.
Fig. 1.13 Energy minimization, pre-equilibration (or relaxation), equilibration, production¶
1.5. Boundary conditions: Open, closed and periodic¶
Computational systems have a very limited number of particles compared to macroscopic systems. This is one of the reasons why it is very difficult and impractical to simulate systems that have real walls or boundaries. In addition, one is often interested in bulk systems, such as bulk solutions of polymers or colloids, or proteins in solution. One additional difficulty in having walls is that they tend to give rise to finite-size effects.
The most common solution is to apply Periodic Boundary Conditions (PBC). The figures below explain the concept.
Fig. 1.14 The most common boundary conditions. Left: Open boundary. The particles a free to move anywhere in space without limitations. Middle: Particles in a box with walls. Here, hard walls are assumed meaning the particles undergo elastic collisions and are reflected back from the boundary. Right: Periodic boundaries. In this case there is no physical wall, but since the system is periodic (not open), the particles have to be wrapped back into the box when they cross the border.¶
Fig. 1.15 Particle motions in system with periodic boundary conditions.¶
1.6. Atomic and molar masses¶
When we set up MD simulations, we need to have estimates, for example, for the size of the simulation box, the number of molecules and the types of molecules. This may be sometimes difficult, but it is easy to get a reasonable estimate and for that atomic and molar masses are needed. As reminder, let’s review the concept of mole and its relation to the mass of a an atom:
Chemical notation
\(^{12}\)C = 1 mole of \(^{12}\)C
Using the old (pre-2019) definition, the atomic mass of \(^{12}\)C is 12 amu. Hence [mass in amu] = 12. That is, one mole of \(^{12}\)C has the atomic mass of 12. To get the mass of a \(^{12}\)C atom, we have to divide by Avogadro’s number:
1.6.1. Historical notes:¶
Avogadro’s number is named after Amadeo Avogadro, an Italian scientist (who started out as a lawyer). Avogadro’s number was originally proposed by Jean Perrin who was also the first to determine it and was awarded the Nobel Prize in Physics in 1926. Avogadro studied gases and proposed that under given thermodynamic conditions, the volume is proportional to the constituents of that gas independent of the precise nature of that gas. In earlier German literature, Avogadro’s number has the name Loschmidt number.
The first standard was the mass of the hydrogen atom (Stanislao Cannizzarro). The problem with this was the lightness of hydrogen which lead to large experimental errors (Perrin also used the hydrogen mass standard). In 1903, the German Chemical Society (Deutsche Chemische Gesellschaft) set the \(^{16}\)O scale.
1.6.2. How to estimate the number of molecules and box size¶
The mole (mol) is defined as the amount of substance that contains Avogadro’s number (\(N_A\)) of constitutive particles (\(N_A \approx 6.0221 \times 10^{23}\,\mathrm{mol}^{-1}\)). The constitutive particles may be molecules or atoms. Importantly, \(N_A\) makes no reference to the their precise nature. The mole is one of the seven SI base units. The older, pre-2019, definition of mole is that it is the amount of chemical substance (atoms, molecules) contained in 12 grams of \(^{12}\)C. The molar mass is defined as mass (typically grams) divided by the amount of substance (in moles). It is thus given in units of g/mol. With this, the unified atomic mass unit can be defined as
where \(M_\mathrm{u}\) is the molar mass constant. In the above, we gave the unified atomic mass in grams since that is the common notation although kilogram would be the more appropriate unit as it is one of the base SI units. In addition, it is good to keep in mind that the atomic radii are about 1 Å while the nuclear radius is about \(10^{-5}\) Å.
Additional information: SI Units
The seven SI base units:
quantity |
name |
symbol |
defining constant |
|---|---|---|---|
time |
second |
s |
hyperfine transition frequency of cesium |
length |
meter |
m |
speed of light |
mass |
kilogram |
kg |
Planck’s constant |
temperature |
kelvin |
K |
Boltzmann’s constant |
amount of substance |
mole |
mol |
Avogadro’s constant |
electric current |
ampere |
A |
elementary charge |
luminous intensity |
candela |
cd |
luminous efficacy of 540 THz radiation |
More information: International System of Units (SI)
1.6.3. Example: Estimate for the number of water molecules and the size of the simulation box¶
The above formulas can now be used to estimate the number of water molecules and the size for the simulation box.
Step 1: Determine the weight of the molecule in grams. For that, its mass in unified atomic mass is needed together with Avogadro’s constant:
Step 2: We need to have some approximate density (\(\rho\)) and number of molecules (\(N_\mathrm{molecule\)}). Since the simulation box is in nanometers, we should convert this to grams/nanometers: \(1\,\mathrm{g/cm^3} = 10^{-21}\,\mathrm{g/nm^3}\):
Step 3: Solve for volume and assume that the simulation box is cubic
This gives the very useful formula for the simulation box size:
Task: Estimate the simulation box size for a given number of water molecules:
Use the above to estimate the (cubic) box size that is needed for 3,000 water molecules. Try to solve this first on your own before seeing the solution.
Solution:
Step 1: The unified atomic mass of water (using table values for the unified atomic masses of hydrogen (1.008 u) and oxygen (15.9994 u)) is
With this the molar mass is
To get the weight of a water molecule in grams, we have to divide by Avogadro’s constant:
Step 2: The density of water is approximately \(1\,\mathrm{g/cm^3}\). We have 3,000 water molecules.
Step 3: Use the formula
Substitution gives
Gromacs notes: Number of water molecules and box size
The Gromacs unit system uses u (\(1.6605402 \times 10^{-27}\) kg) and nanometers so the above can be applied directly.
If you have no table available, Gromacs provides unified atomic masses in the file
$GMXDATA/top/atommass.dat
and toward the end of the file there is an entry for water with the following values for oxygen and hydrogen (of course you can check these from elsewhere as well):
SOL OW 15.9994
SOL HW 1.008