Truncation Error in Taylor’s series
Contents
Truncation Error in Taylor’s series¶
Most algorithms in Numerical Analysis suffer from some form of truncation error. Often this truncation error comes about from some series solution to the problem of interest that we truncate at some finite order in order to solve. To illustrate the concept of a truncation error, let’s look at an example for Taylor’s series. It is helpful to recall Taylor’s theorem from first year calculus:
Taylor’s Theorem¶
Suppose we have a function \(f\in C^n[a,b]\) (i.e. \(f\) is \(n\) times continuously differentiable), that \(f^{(n+1)}\) exists on \([a,b]\) and \(x_0\in [a,b]\). Then for \(x\in [a,b]\) we have
provided \(R_n\rightarrow 0\) as \(n\rightarrow \infty\), where the truncation error (from truncating the series at the \(n\)’th term is
for some \(\xi \in [x_0,x]\).
Note that
\(R_n\) could be positive or negative so the absolute error, \(|R_n|\) is usually what one would quote for the error.
we do not usually know what \(\xi\) is, other than it is in \((x_0,x)\). However, if we can guess \(max|f^{(n+1)}(x)|\) on \([a,b]\) then we can bound the absolute error.
Example¶
Let’s construct the Taylor series and bound the truncation error for the function \(f(x)=1/(1+x)\) about \(x_0=0\). First note that \(f^{(n)}(x)=\frac{(-1)^n}{(1+x)^{n+1}}\). So, using Taylor’s theorem, we see that
and in this case the truncation error is
To bound the truncation (absolute) error, we need to consider a few points:
We need an interval over which we are considering the Taylor series. In this case the series only converges for \(|x|<1\) so let’s assume \(x \in [0,1)\) (i.e. the \(a\) and \(b\) in Taylor’s theorem will be taken to be \(a=0\) and \(b=1\)).
It is ok if the bound in \(|R_n|\) depends on \(x\) as we will certainly know what \(x\) is. However, the only thing we know about \(\xi\) is that it must be in the interval \([0,x)\). So to bound the error, we first must bound the deriviative \(|f^{(n+1)}(x)|=|\frac{(-1)^(n+1)}{(1+x)^{n+1}}|=\frac{1}{(1+x)^{n+1}}\). To get an idea of how to do this, a plot is always a good place to start.
from matplotlib import pyplot as plt
import numpy as np
x = np.arange(0, 1, 0.05)
plt.plot(x,1/(1+x))
plt.plot(x,1/(1+x)**2)
plt.plot(x,1/(1+x)**3)
plt.plot(x,1/(1+x)**4)
plt.xlabel(r'$\xi$')
plt.ylabel(r'$1/(1+\xi)^{n+2}$')
plt.show()
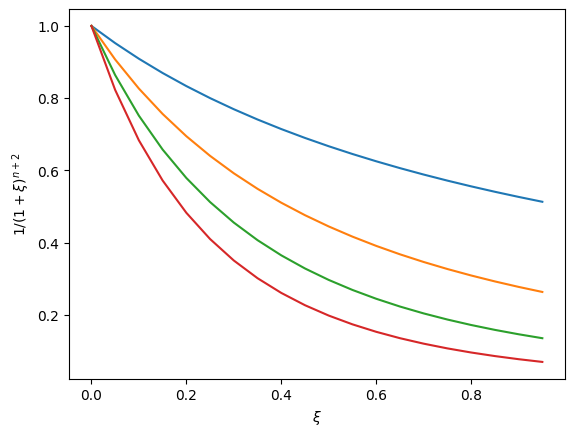
From the plot it is clear that \(\frac{1}{(1+x)^{n+1}}\) is a monotonically decreasing function on the interval \([0,1]\) and that its maximum is at its leftmost endpoint, \(x=1\) where it takes the value 1 independent of \(n\). Plugging this into the bound on the absolute error gives